Cet article est la suite de mon article présentant les PRNG, les CSPRNG et l’entropie. Il a pour but de présenter l’implémentation que j’ai faite pour mon projet d’ADA d’un CSPRNG-like
Source d’inspiration
Pour la création de mon CSPRNG, je me suis beaucoup inspiré d’une part du générateur de pseudo-aléatoire de Linux, /dev/random, et d’autre part de The Linux PseudoRandom Number Generator Revisited. Ce dernier est un rapport publié en 2012 par 4 chercheurs sur le fonctionnement du CSPRNG de Linux, avec une analyse de sécurité. Je vous en conseille fortement sa lecture, tant il est passionant et relativement accessible.
Le générateur de pseudo-aléatoire de linux est situé dans le fichier drivers/char/random.c, et j’ai principalement utilisé cette interface pour m’y retrouver et naviguer dans le code du kernel facilement.
Le CSPRNG
Pour des raisons de simplicité, et en tenant compte de diverses contraintes auxquelles j’ai du faire face, j’ai bien évidemment adapté ce générateur pour le simplifier et le faire correspondre plus précisemment à nos besoins.
Attention ! La première règle lors de lecture de documentation sur la cryptographie est ne cherchez pas à réimplémenter les choses vous-mêmes, vous allez vous planter. Je ne prétends pas pouvoir déroger à cette règle, et je peux même affirmer de manière quasi-certaine que le CSPRNG que je présente ici n’en est pas un, et possède des failles d’implémentation (j’en possède quelques unes en tête). Néanmoins, je considère ce travail comme étant intéressant, comme étant une bonne approche pour se familiariser avec des concepts de cryptographie, et je vous déconseille donc de l’utiliser pour des projets sérieux pour lesquels la sécurité est vraiment importante
La pool d’entropie
De la perception que je peux avoir du générateur de Linux, tout s’articule autours de la pool d’entropie.
En réalité, comme présenté dans The Linux PseudoRandom Number Generator Revisited, Linux possède 3 pool d’entropies, une “principale” et deux autres pour /dev/random et pour /dev/urandom. Je me suis contenté d’une seule pool, ce qui me semblait largement suffisant
Une pool d’entropie peut se représenter comme une sorte de gros tableau de taille fixe dans lequel on va mélanger de l’aléatoire. De la même manière qu’une piscine, la taille du tableau est fixe, mais la quantité d’entropie contenue dedans (l’eau de la pisicne pour poursuivre l’analogie) peut varier.
Cette piscine d’entropie, d’aléatoire donc, représente l’état interne de notre PRNG. Le contenu de cette piscine d’entropie ne doit pas être divulgué, pour éviter de perdre en sécurité.
Pour notre implémentation, je me suis orienté vers une pool consituée d’un tableau de 64 uint32_t. La quantité maximale d’entropie est donc de 64 * 32 bits, ce qui semble suffisant.
La collecte d’entropie
Pour collecter de l’entropie, il faut essayer de trouver des sources de “pur” aléatoire qui seraient disponibles sur notre système. Notre projet étant prévu pour une carte embarquée, cette dernière dispose d’un accéléromètre 3 dimensions, qui semble être un bon candidat pour extraire des bits d’aléatoire pur, via les légers mouvements qu’il détecte de manière permanente, et le bruit naturel des capteurs.
Pour récupérer les informations du gyroscope, on se base sur les bibliothèques ADA fournies, donc l’une qui nous expose plusieurs interfaces Gyro pour configurer l’accéléromètre et récupérer des valeurs :
-- variables
Axes : L3GD20.Angle_Rates;
Last_Axes : L3GD20.Angle_Rates;
-- Configuration du Gyro
STM32.Board.Initialize_Gyro_IO;
Gyro.Reset;
Gyro.Configure
(Power_Mode => L3GD20_Mode_Active,
Output_Data_Rate => L3GD20_Output_Data_Rate_760Hz,
Axes_Enable => L3GD20_Axes_Enable,
Bandwidth => L3GD20_Bandwidth_1,
BlockData_Update => L3GD20_BlockDataUpdate_Continous,
Endianness => L3GD20_Little_Endian,
Full_Scale => L3GD20_Fullscale_2000);
Gyro.Enable_Low_Pass_Filter;
Gyro.Set_FIFO_Mode (L3GD20_Stream_Mode);
-- Collecte de l'état actuel du Gyro
Gyro.Get_Raw_Angle_Rates (Axes);Il suffit de collecter périodiquement l’état actuel de l’accéléromètre et calculer le delta entre 2 valeurs. Avec ce delta, on a réussi à récupérer une source d’aléatoire, et on a des valeurs prêtes à être exploitées, via notre fonction de mixage.
La board, en train de collecter de l’entropie dans sa pool grâce à l’accéléromètre. En la remuant, j’augmente le delta mesuré (première ligne), pour remplir plus vite l’entropie contenue dans la board (ligne 3)
La fonction de mixage
Pour pouvoir intégrer ces quelques bits d’aléatoire issu du capteur, il faut utiliser une fonction de mixage. Cette fonction s’occupe de mélanger la pool et d’y intégrer ces quelques bits, pour les répartir et éviter “d’écraser” l’aléatoire déjà présent dedans. Pour procéder ainsi, je me suis inspiré encore une fois de la fonction de mixage de linux pour écrire la mienne.
Cette fonction prend en argument un int d’entropie à intégrer, et la struct représentant ma pool (avec son state). On itère sur des groupes de 8 bits de l’int (char par char), et chaque octet est d’abord rol32 selon un facteur variable, puis est intégré à la pool grâce à un Linear Feedback Shift Register.
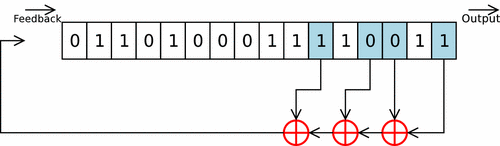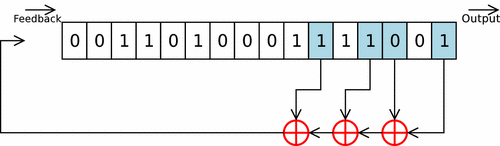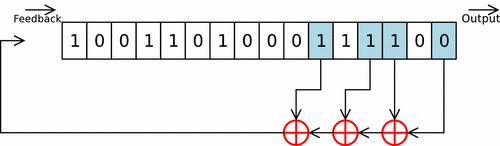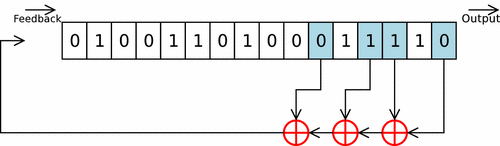
Les paramètres du LFSR sont les mêmes que celui de linux, en tenant compte du fait que celui-ci est conçu pour une piscine de 128 uint32_t (contre 64 pour la mienne). Ces paramètres ne sont donc pas optimaux pour ce cas concret, mais je m’en contenterai.
L’octet ainsi obtenu n’est pas directemnt intégré dans la pool, mais est d’abord légérement modifé. Les 3 bits de poids faible sont envoyé dans une twist table, permettant d’effectuer rapidement une multiplication sur GF(2^32) (lookup-table). Le Linux PseudoRandom Number Generator Revisited explique que cette twist table permet de respecter les recommendations des polynômes CRC-32-IEEE 802.3. Les 29 bits de poids forts sont eux shiftés de 3 vers la droite, et le tout est XORé.
Le code de la fonction est donc le suivant :
#define POOL_SIZE 64
#define _WORD_MASK (POOL_SIZE - 1)
struct entropy_pool {
uint32_t pool[POOL_SIZE];
uint32_t entropy_count;
// Entropy mixing
uint8_t i; // Where to put the created entropy. Init it to 0, and don't touch
int rotate; // Number of rol32 rotation to perform
}
static uint32_t const twist_table[8] = {
0x00000000, 0x3b6e20c8, 0x76dc4190, 0x4db26158,
0xedb88320, 0xd6d6a3e8, 0x9b64c2b0, 0xa00ae278 };
static uint32_t const taps[] = {
128, 104, 76, 51, 25, 1
}; // P(X) = X^128 + X^104 + X^76 + X^51 + X^25 + X + 1
// Q(X) = alpha^3 (P(X) - 1) + 1 with alpha^3 compute using twist_table
// Mix some entropy in the entropy pool
void mix_pool(int entropy, struct entropy_pool *pool)
{
char *entropy_bytes = (void *)(&entropy);
uint32_t w;
for (uint8_t i = 0; i < sizeof(int); ++i)
{
char byte = entropy_bytes[i];
w = rol32(byte, pool->rotate);
pool->rotate = (pool->rotate + 7) & 31;
pool->i = (pool->i - 1) & _WORD_MASK;
for (uint8_t j = 0; j < 6; ++j)
w ^= pool->pool[(pool->i + taps[j]) & _WORD_MASK]; // LFSR
pool->pool[pool->i] = (w >> 3) ^ twist_table[w & 7];
}
}La fonction d’extraction
L’étape suivante pour avoir un CSPRNG qui fonctionne et qui est utilisable, est d’avoir un moyen de pouvoir extraire de l’entropie de notre pool, et de la renvoyer sous forme de bits pseudo-aléatoires.
De la même manière que pour Linux, ma fonction pour extraire de l’aléatoire de la pool procède en plusieurs étapes :
- Un hash de la pool entière est effectué avec chacha20
- Chacha20 n’étant pas une fonction de hashage, le résultat produit est plié sur un tableau de 4
uint32_t(avec des super XOR) - Le hash est mis de coté, et est remixé dans la pool en utilisant la fonction d’insertion présenté ci-dessus
- Un extrait de la pool est de nouveau pris, à un index variable
- Cet extrait de 4
uint32_test XORé avec le hash de la pool, et est plié sur 2uint32_t - Ce résultat final est renvoyé, un byte à la fois, à l’utilisateur
Le code est le suivant, en reprenant et modifiant l’extrait de code précédant :
struct entropy_pool {
uint32_t pool[POOL_SIZE];
uint32_t entropy_count;
// Entropy mixing
uint8_t i; // Where to put the created entropy. Init it to 0, and don't touch
int rotate; // Number of rol32 rotation to perform
// Entropy extraction
uint8_t j; // Where to get the last 16 bytes of entropy to XOR. Init it to 0, and don't touch
uint32_t chacha20_state[16];
uint8_t chacha20_init; // Is chacha20_state initialized ?
uint32_t output[2]; // Contains (remaining_extracted) random bytes to be given to the user
uint8_t remaining_extracted;
};
static uint8_t _give_random_byte(struct entropy_pool *pool)
{
uint8_t i = pool->remaining_extracted >= 4;
uint8_t j = pool->remaining_extracted % 4;
pool->remaining_extracted--;
uint8_t random[4];
_memcpy(random, pool->output + i, 4);
return random[j];
}
static void init_chacha20(struct entropy_pool *pool)
{
// Init chacha20 state from the entropy pool
_memcpy(pool->chacha20_state, pool->pool, sizeof(uint32_t) * 16);
for (uint8_t i = 16; i < POOL_SIZE; ++i)
pool->chacha20_state[i % 16] ^= pool->pool[i];
pool->chacha20_state[12] = 1; // Set the block counter
pool->chacha20_state[13] = 0; // Set the block counter
pool->chacha20_init = 1;
}
uint8_t get_random(struct entropy_pool *pool)
{
if (pool->remaining_extracted > 0)
return _give_random_byte(pool);
if (!pool->chacha20_init)
init_chacha20(pool);
// Hash the whole entropy pool
uint32_t hash_all[16] = {0};
for (uint8_t i = 0; i < POOL_SIZE; i += 16)
{
uint32_t key_stream[16];
chacha20(pool->chacha20_state, key_stream);
for (uint8_t j = 0; j < 16; ++j)
{
if (unlikely(i == 0))
hash_all[j] = (key_stream[j] ^ pool->pool[i + j]);
else
hash_all[j] ^= (key_stream[j] ^ pool->pool[i + j]);
}
}
uint32_t hash[4] = {0};
// Fold the 64 bytes hash in a 16 bytes hash
for (uint8_t i = 0; i < 4; ++i)
hash[i] = hash_all[i];
for (uint8_t i = 4; i < 16; ++i)
hash[i & 3] ^= hash_all[i];
// Change some of the chacha20 state
pool->chacha20_state[hash_all[0] % 12] ^= hash_all[1]; //uint32_t of the key
pool->chacha20_state[(hash_all[2] & 1) + 14] ^= hash_all[3]; //uint32_t of the nonce
//Mix the hash back in the pool
for (uint8_t i = 0; i < 4; ++i)
{
int32_t val = hash[i];
mix_pool(val & 0x000000FF, pool);
mix_pool(val & 0x0000FF00, pool);
mix_pool(val & 0x00FF0000, pool);
mix_pool(val & 0xFF000000, pool);
}
uint32_t entropy_extract[4];
_memcpy(entropy_extract, pool->pool + pool->j, 16);
pool->j = (pool->j + 16) % POOL_SIZE;
// Xor and fold
pool->output[0] = (entropy_extract[0] ^ hash[0]) ^ (entropy_extract[2] ^ hash[2]);
pool->output[1] = (entropy_extract[1] ^ hash[1]) ^ (entropy_extract[3] ^ hash[3]);
pool->remaining_extracted = 8; // We have 2 uint32_t so 8 bytes of data
credit_entropy(-64, pool);
return _give_random_byte(pool);
}Ce code est évidemment perfectible, mais c’est déjà un bon début pour extraire des valeurs aléatoires.
On notera l’utilisation d’une fonction maison, credit_entropy, à la fin de la fonction. Cette fonction est utilisée pour mettre à jour le compteur d’entropie de la pool, présenté par la suite.
A propos de chacha20
Chacha20 est un algorithme de chiffrement par flot qui date de 2008. Cet algorithme possède plusieurs caractéristiques, notamment celle d’être assez rapide à implémenter et surtout d’être très rapide car assez simpliste. En revanche, malgré sa simplicité, l’algorithme est néanmoins sûr. Il existe plusieurs cryptanalises qui ont été effectué, et aucune n’a fait part de véritable problèmes avec Chacha20. Comme souvent dans ce genre de cas, cela signifie qu’il existe potentiellement des faiblesses dans l’algorithme qui ne sont pas connues, mais qu’il est bien plus probable que les faiblesses viennent d’erreurs d’implémentations, souvent par canaux auxilliaire comme des attaques temporelles.
Ici Chacha20 est utilisé comme fonction de hashage, ce qui est un usage un peu détourné, pour certaines raisons. La première est la simplicité d’implémentation de Chacha20 : seulement quelques dizaines de lignes. De plus, Chacha20 est une fonction de chiffrement par flot qui est très performante, et qui fonctionne donc très bien sur du matériel embarquée. Par ailleurs, les propriétés de cette fonction de chiffrement dans l’utilisation que j’en ai sont très similaires à une fonction de hashage :
- Pas de possibilité de revenir en arrière (car il faudrait la clé, et celle-ci est modifiée au fur et à mesure)
- Obtention d’un résultat assimilable à une empreinte
- Probabilité réduite de collisions, et bonne distribution des résultats parmi l’ensemble des probabilités
rngtest-ons chacha20
Même si effectivement certains raccourcis sont pris et certaines approximations sont faites (encore une fois, ce que je présente n’a pas pour but d’être parfaitement robuste face à n’importe quelle attaque (et ne l’est pas !), ne faites pas confiance à mon algorithme sorti à moitié de mon chapeau si vous êtes paranos (ou juste sain d’esprit)), on peut avoir une approximation de la véracité du dernier point présenté juste au dessus assez facilement :
$ cat /dev/urandom | openssl enc -chacha20 -e -pbkdf2 -k thisisatest | rngtest
....
rngtest: bits received from input: 27487380032
rngtest: FIPS 140-2 successes: 1373219
rngtest: FIPS 140-2 failures: 1150
rngtest: FIPS 140-2(2001-10-10) Monobit: 130
rngtest: FIPS 140-2(2001-10-10) Poker: 141
rngtest: FIPS 140-2(2001-10-10) Runs: 439
rngtest: FIPS 140-2(2001-10-10) Long run: 447
rngtest: FIPS 140-2(2001-10-10) Continuous run: 0
rngtest: input channel speed: (min=108.991; avg=13496.076; max=19073.486)Mibits/s
rngtest: FIPS tests speed: (min=29.344; avg=174.900; max=205.091)Mibits/s
rngtest: Program run time: 151934446 microsecondsrngtest est un binaire permettant de tester la répartition aléatoire d’un bloc de données, en suivant les recommendations de la FIPS 140-2. En l’occurence, je teste un flux de données pseudo-aléatoire chiffré par flux avec chacha20 grâce à openssl (avec un super mot de passe). Les résultats de rngtest sont assez bons (0.08% d’échec pour les blocs, ce qui est faible et proche du taux d’échec de /dev/urandom lui même).
De plus, j’étais curieux de découvrir Chacha20 concrètement, et vu les contraintes qui me sont imposées pour ce projet, il est clairement plus marrant d’utiliser Chacha20 qu’un banal sha1. (bouuuh sha1, bouh !).
Comptons de l’entropie
Un lecteur aggueri aura remarqué la présence dans ma struct entropy_pool d’une valeur entropy_count. En effet, il est bien beau d’avoir une piscine remplie d’aléatoire, mais il est plus d’intéressant d’avoir une piscine remplie d’aléatoire disposant d’une sonde indiquant à la louche combien “d’aléatoire” j’ai dedans.
C’est donc le rôle de cet attribut, dont la valeur n’est censé varier qu’entre 0 et ma superbe macro MAX_ENTROPY qui a pour valeur (POOL_SIZE << (5 + ENTROPY_SHIFT)), genre à peu près le nombre de bits qu’il y a dans la pool, fois 8 (explications plus tard).
Ce compteur n’a pas pour but d’être modifé manuellement, mais plutôt via la fonction int credit_entropy(int nb_bits, struct entropy_pool *pool) et sa petite soeur bien utile, int entropy_estimator(int x).
entropy_estimator
Dans le fonctionnement de mon PRNG, il n’est pas du ressort de la fonction d’ajout de créditer de l’entropie, mais de l’appelant de le faire.
Mon PRNG étant fortement inspiré de celui de Linux, l’ajout d’entropie nulle dans la pool n’est pas censé réduire l’entropie. Il est prouvé pour la fonction de mixage de linux que l’entropie de la piscine après ajout est au moins égale à l’entropie de la piscine avant ajout (avec des subtilités rigolotes, mais je vous invite une fois de plus à lire The Linux PseudoRandom Number Generator Revisited pour ça).
Ainsi, un utilisateur désirant ajouter de l’entropie dans la piscine peut le faire sans se soucier outre-mesure de la potentiel piètre qualité de son entropie, car le compteur ne sera pas nécéssairement incrémenté. Plus précisement, dans le pire des cas, l’entropie réelle de la piscine n’est pas augmentée (car l’entropie ajoutée était effectivement basse) et son compteur non plus. Dans le meilleur - mais pessimiste - des cas l’entropie réelle augmente, et le compteur reste tel quel.
L’estimation de la quantité d’entropie contenue dans un int dépend évidemment de la source, mais dans mon cas la source est unique (du moins pour le moment, j’espère recevoir du matériel … spécial, pour obtenir une autre source d’entropie, dans un futur proche), donc la fonction aussi. Cette dernière est également inspirée de l’estimation pessimiste de l’entropie ajoutée dans linux pour des sources variées, comme celle des variations des cycles d’horloges.
Voici le code de celle ci, où X est l’entropie désireuse d’être ajoutée :
/*
Estimate the amount of bits of entropy in x, a delta.
returns
| 0 for x < 8
| 12 for x > 4096
| floor(log2(x)) else
*/
int entropy_estimator(int x)
{
if (x < 8)
return 0;
if (x > 4096) // 2^12
return 12;
int cnt = 3;
while (x > 8)
{
cnt++;
x >>= 1;
}
return cnt - (x != 8);
}credit_entropy
Une fois le nombre de bits d’entropie à ajouter comptabilisé, ce dernier est crédité via une fonction credit_entropy. Cette dernière s’assure que le compteur ne dépasse pas les limites [0, MAX_ENTROPY], et calcule la quantité réelle d’entropie à ajouter. En effet, plus la piscine est remplie, plus “l’aléatoire se marche sur les pieds” pour parler par analogie. Il est plus difficile d’ajouter réellement de l’aléatoire quand la grosse majorité des bits sont déjà aléatoires. La fonction credit_entropy tente donc, toujours en s’inspirant du travail fait pour le PRNG de linux, de rendre compte de cet effet.
Il est intéressant de noter qu’à cause de cet effet, l’entropie à rajouter est souvent légèrement inférieure au nombre entier juste au dessus. Par exemple, si la pool contient 1 bit d’entropie, le calcul du nombre réel de bits d’entropie à ajouter pour un appel à credit_entropy avec 8 bits à crédite donnera une valeur proche de 7.98. Il serait donc dommage de perdre le crédit des 0.98 bits en arrondissant à 7, mais cela semble néanmoins être une mauvaise idée que de créditer plus que ce qui est réellement apporté.
Pour cette raison, le compteur d’entropie tiens également compte de 8ième de bits. Ainsi, la macro ENTROPY_SHIFT permet le passage de nombre entiers de bits à des 8ièmes de bits. Ainsi, pour reprendre l’exemple d’au dessus, 7.875 bits seront réellement crédités.
Encore une fois, je ne suis (malheureusement) pas l’auteur de cette idée, et je ne fais que l’emprunter à Linux, toujours en adaptant pour mes besoins :
// Allow us to take into account fractions of bits of entropy
#define ENTROPY_SHIFT 3
#define ENTROPY_COUNT(x) ((x) >> ENTROPY_SHIFT)
// Maximum of entropy in the pool, taking account of partial bits of entropy.
// shift << 5 is for 32 (since there are 32 bits in a uint32_t
#define MAX_ENTROPY (POOL_SIZE << (5 + ENTROPY_SHIFT))
// log(POOL_SIZE) + 5
// Used for faster division by bitshift
#define POOL_BIT_SHIFT (6 + 5)
enum { EMPTY = 0, LOW = 1, MEDIUM = 2, FILLED = 3, FULL = 4 };
// entropy <- entropy + (MAX_ENTROPY - entropy) * 3/4 * add_entropy / MAX_ENTROPY
int credit_entropy(int nb_bits, struct entropy_pool *pool)
{
int add_entropy = nb_bits << ENTROPY_SHIFT;
if (unlikely(add_entropy > MAX_ENTROPY / 2))
{
// The given above formula is a faster approximation that cannot
// work if add_entropy > MAX_ENTROPY / 2
credit_entropy(nb_bits / 2, pool);
return credit_entropy(nb_bits / 2, pool);
}
else if (likely(add_entropy > 0))
{
const int s = POOL_BIT_SHIFT + ENTROPY_SHIFT + 2; // +2 is the /4 in the above formula
add_entropy = ((MAX_ENTROPY - pool->entropy_count) * add_entropy * 3) >> s;
}
int new_entropy_count = pool->entropy_count + add_entropy;
if (new_entropy_count <= 0)
{
pool->entropy_count = 0;
return EMPTY;
}
if (unlikely(new_entropy_count >= MAX_ENTROPY))
{
pool->entropy_count = MAX_ENTROPY;
return FULL;
}
pool->entropy_count = new_entropy_count;
return (int)(((float)new_entropy_count / (float)MAX_ENTROPY) * 3) + 1;
}La fonction renvoie une enum, utilisée pour savoir côté ADA à quel point la piscine d’entropie est pleine. (EMPTY et FULL sont les extrêmes, et les 3 valeurs restantes se séparent chacune un tiers).
Résultats
Les résultats obtenus via ce pseudo-CSPRNG sont en réalité assez satisfaisant, et largement suffisant pour nos besoins de génération de nombre premiers. Le pourcentage de blocks non-retenus par rngtest est de 0.35% en moyenne, là où /dev/urandom se situe autours des 0.09% (facteur 4 donc). Il faut d’ailleurs retenir que ce test n’est qu’un indicateur, et n’est ni nécéssaire ni suffisant pour indiquer une quelconque faiblesse dans un CSPRNG, tant les vecteurs d’attaques sont nombreux.
En pratique, il m’a fallut plusieurs journées de travail pour débroussailler le terrain, comprendre l’implémentation de linux, les optimisations qui sont faites, réduire le scope de ce dont j’avais réellement besoin et l’implémenter. Je suis assez satisfait du résultat obtenu, car même si je sais que mon implémentation ne tiendrai pas vraiment la route face à un adversaire avec beaucoup (du moins je l’espère !) de moyens, l’implémentation tiens compte de contraintes de la carte, est capable de trouver sa source d’entropie et fonctionne au final très bien.
Le code au total fait quelques centaines de lignes - ce qui est finalement assez peu -, même s’il est perfectible. Je pense le mettre en ligne quelque part dans un futur proche, où les PR seront les bienvenues.

Leave a Comment
Your email address will not be published. Required fields are marked *